¿Cómo se resuelve una ecuación de segundo grado?
Son expresiones matemáticas que involucran una variable elevada al cuadrado

Ecuación de segundo grado. | Freepik
Las matemáticas están presentes en cada rincón de nuestra vida, desde las simples operaciones aritméticas que utilizamos a diario hasta los algoritmos que hacen funcionar nuestros dispositivos electrónicos. Son la base de la ingeniería, la física, la economía y muchas otras disciplinas.
Aprender matemáticas no solo nos permite resolver problemas prácticos, sino que también desarrolla nuestro pensamiento crítico y nuestra capacidad de abstracción. Es una herramienta indispensable para tomar decisiones informadas y navegar por el mundo moderno.
¿Qué son las ecuaciones de segundo grado?
Son expresiones matemáticas que involucran una variable elevada al cuadrado (x²), además de otros términos que pueden incluir la variable elevada a la primera potencia (x) y una constante. Se representan de la siguiente manera:
- ax² + bx + c = 0
Donde:
- a, b y c son números conocidos llamados coeficientes.
- a debe ser diferente de cero para que sea una ecuación de segundo grado.
- x es la incógnita que queremos encontrar.
¿Por qué son importantes?
Las ecuaciones de segundo grado tienen una amplia variedad de aplicaciones en diversos campos, como:
- Física: se utilizan para modelar el movimiento de proyectiles, el crecimiento de poblaciones y muchos otros fenómenos.
- Ingeniería: son esenciales para el diseño de estructuras, circuitos eléctricos y sistemas de control.
- Economía: se emplean en modelos de oferta y demanda, optimización de recursos y análisis financiero.
- Geometría: se utilizan para calcular áreas, volúmenes y resolver problemas relacionados con figuras geométricas.
¿Cómo se resuelven?
Existen diferentes métodos para resolver ecuaciones de segundo grado, siendo el más conocido la fórmula general:
- x = (-b ± √(b² – 4ac)) / (2a)
Esta fórmula nos permite encontrar los valores de x que satisfacen la ecuación.
¿Qué tipos de soluciones pueden tener?
Dependiendo de los valores de los coeficientes a, b y c, una ecuación de segundo grado puede tener:
- Dos soluciones reales distintas: cuando el discriminante (b² – 4ac) es mayor que cero.
- Una única solución real: si el discriminante es igual a cero.
- Ninguna solución real: cuando el discriminante es menor que cero. En este caso, las soluciones son números complejos.
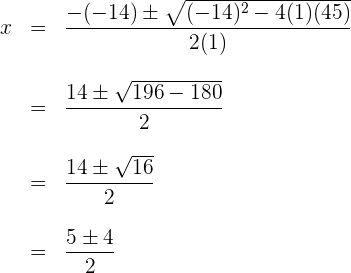
Ejemplos resueltos
Resuelve la siguiente ecuación: 2x² – 5x + 3 = 0
Solución: identificamos los valores de a, b y c:
- a = 2
- b = -5
- c = 3
Sustituimos en la fórmula general: x = (-(-5) ± √((-5)² – 423)) / (2*2) x = (5 ± √(1)) / 4
Tenemos dos soluciones:
- x₁ = (5 + 1) / 4 = 3/2
- x₂ = (5 – 1) / 4 = 1
Solución: x = 3/2 o x = 1
Ejemplo de factorización
Resuelve la siguiente ecuación: x² – 7x + 12 = 0
Solución: buscamos dos números que multiplicados den 12 y sumados den -7. Estos números son -3 y -4.
Entonces, factorizamos la ecuación: (x – 3)(x – 4) = 0
Igualamos cada factor a cero:
- x – 3 = 0 → x = 3
- x – 4 = 0 → x = 4
Solución: x = 3 o x = 4
Ejemplo 3: completando el cuadrado
Resuelve la siguiente ecuación: x² + 6x + 2 = 0
Solución:
- Pasamos el término independiente al otro lado: x² + 6x = -2
- Sumamos y restamos el cuadrado de la mitad del coeficiente de x: x² + 6x + 9 – 9 = -2
- Factorizamos el trinomio cuadrado perfecto: (x + 3)² = 7
- Aplicamos raíz cuadrada a ambos lados: x + 3 = ±√7
- Despejamos x: x = -3 ± √7
Solución: x = -3 + √7 o x = -3 – √7
¿Qué es el discriminante?
En una ecuación cuadrática de la forma ax² + bx + c = 0, el discriminante se representa con la letra griega delta (Δ) y se calcula de la siguiente manera:
Δ = b² – 4ac
¿Para qué sirve el discriminante?
El discriminante nos proporciona información valiosa sobre las soluciones de la ecuación cuadrática, sin necesidad de resolverla completamente. Específicamente, nos indica la naturaleza de las raíces (o soluciones):
- Si Δ > 0: la ecuación tiene dos soluciones reales distintas. Esto significa que la parábola correspondiente a la ecuación corta al eje de las x en dos puntos diferentes.
- Si Δ = 0: la ecuación tiene una única solución real (raíz doble). En este caso, la parábola es tangente al eje de las x.
- Si Δ < 0: esta ecuación no tiene soluciones reales. Las soluciones son números complejos. Gráficamente, esto significa que la parábola no corta al eje de las x.
¿Qué son las ecuaciones de segundo grado incompletas?
Son aquellas ecuaciones cuadráticas en las que falta uno o dos de sus términos. Recordemos que la forma general de una ecuación de segundo grado es:
ax² + bx + c = 0
Donde:
- a, b y c son números reales, y
- a es diferente de cero.
Los distintos tipos
Sin término lineal (b = 0):
- ax² + c = 0
Sin término independiente (c = 0):
- ax² + bx = 0
¿Cómo se resuelven?
Cada tipo se resuelve de una manera particular:
Sin término lineal:
- Se despeja x² y se aplica raíz cuadrada a ambos lados, recordando que una ecuación de segundo grado puede tener dos soluciones.
- Ejemplo: 2x² – 8 = 0
- 2x² = 8
- x² = 4
- x = ±√4
- x = 2 o x = -2
Sin término independiente:
- Se factoriza la x y se iguala cada factor a cero.
- Ejemplo: 3x² + 6x = 0
- 3x(x + 2) = 0
- 3x = 0 o x + 2 = 0
- x = 0 o x = -2
Ejemplo resuelto:
Resuelve la ecuación: 5x² = 45
- Despejamos x²: x² = 9
- Aplicamos raíz cuadrada: x = ±√9
- Soluciones: x = 3 o x = -3

